ТРАНСПОНИРОВАНИЕ
МАТРИЦ.
УМНОЖЕНИЕ МАТРИЦ.
I. Транспонирование матриц
Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
Пример 1. Составить транспонированную матрицу, полученную из А:
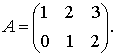
Решение: Поменяем местами строки и столбцы, сохраняя порядок:
Примеры для самостоятельного решения:
Составить из исходной матрицы
транспонированную матрицу:
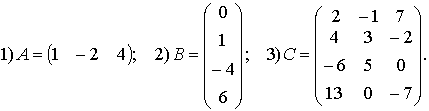
II. Умножение матриц
Пример 1. Рассмотрим для начала простейший пример, когда необходимо
найти произведение двух матриц А и В размером 2´2,
если
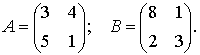
Решение:
Элементы матрицы С находятся по следующему алгоритму:
Элемент матрицы С, стоящий на первой строке, в первом столбце находится как сумма произведений первой строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на первой строке, во втором столбце находится как сумма произведений первой строки матрицы А на второй столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, в первом столбце находится как сумма произведений второй строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, во втором столбце находится как сумма произведений второй строки матрицы А на второй столбец матрицы В.
Таким образом, мы получили
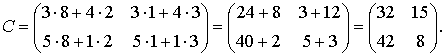
То есть мы получили, что
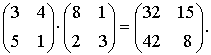
Пример 2. Найдем результат произведения двух матриц
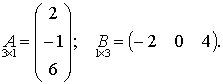
Решение:
то есть мы должны получить матрицу
размера 3´3.
Пример 3. В предыдущем примере мы рассмотрели случай умножения
матрицы А на матрицу В, а в данном примере рассмотрим
случай произведения матрицы В
на А.
Решение:
Пример 4. Найти произведение двух матриц:
Решение: В первом случае найдем произведение:
Во втором случае найдем
произведение:
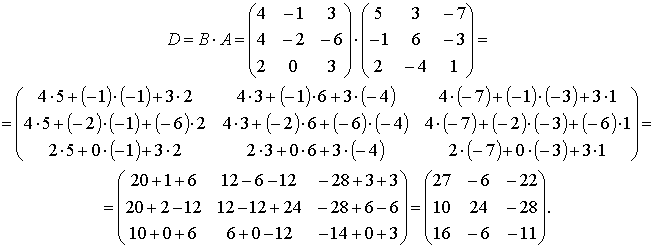
Пример 5. Вычислить значение многочлена 
от матрицы
Решение. В многочлен 
подставим вместо
х матрицу А, вместо числа 3 используем матрицу
3Е, где Е – единичная матрица 2-го порядка
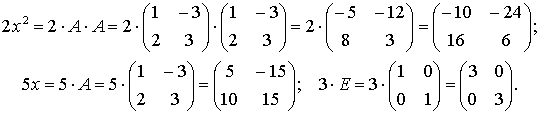
Теперь получим окончательный результат
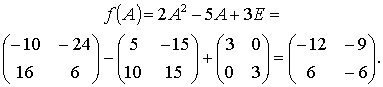
III. Примеры для
самостоятельного решения
II. Найти значение многочлена 
от матрицы А
