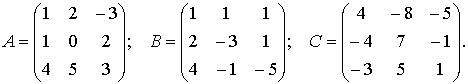МИНОР.
АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ.
I. Минор
Минором
элемента 
матрицы n-го порядка
называется определитель матрицы (n-1)-го порядка, полученный из
матрицы А вычеркиванием i-й строки и j-го столбца.
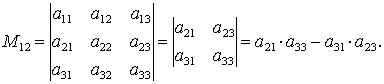
При выписывании определителя (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.
Пример 1. Составить минор 
, полученную из исходной матрицы:
Решение:
.
II. Алгебраические дополнения
Алгебраическим дополнением Аij элемента аij матрицы n-го
порядка называется его минор, взятый со знаком, зависящий от номера строки и
номера столбца:
то есть алгебраическое дополнение
совпадает с минором, когда сумма номеров строки и столбца – четное число, и
отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Пример 1. Найти алгебраические дополнения всех элементов матрицы
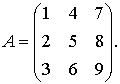
Решение:
III. Примеры для
самостоятельного решения
